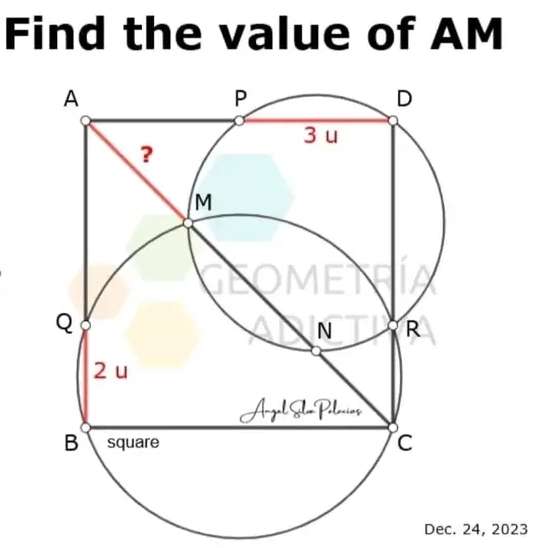
Mathematics Question and Solution
Calculating a, radius of the small circle.
b = c
2a = 3+2c
2a-2c = 3
2c = 2a-3
c = ½(2a-3) --- (1).
d = a-½(c)
d = ½(2a-c) units.
It implies;
a² = 1.5²+(½(2a-c))²
a² = (9/4)+¼(4a²-4ac+c²)
4a² = 9+4a²-4ac+c²
4ac = 9+c² --- (2).
Substituting (1) in (2) to get a, radius of the small circle.
4a(½(2a-3)) = 9+(½(2a-3))²
2a(2a-3) = 9+¼(4a²-12a+9)
16a²-24a = 36+4a²-12a+9
12a²-12a-45 = 0
4a²-4a-15 = 0
Resolving the above quadratic equation via factorization approach to get a, radius of the small circle.
4a²-10a-6a-15 = 0
2a(2a-5)-3(2a-5) = 0
(2a-3)(2a-5) = 0
It implies;
2a-5 = 0
a = ½(5) units.
a = 2.5 units.
2a, diameter of the small circle is;
2*½(5)
= 5 units.
Recall.
c = ½(2a-3)
And a = 2.5 units.
c = ½(2*2.5-3)
c = ½(5-3)
c = 1 unit.
e = 2a-c
e = 5-1
e = 4 units.
e is DR = AQ.
The square side length, ABCD is;
AB = 2+e
AB = 6 units.
f² = 2²+6²
f = √(40)
f = 2√(10) units.
f is CQ, diameter of the big circle.
g = ½(f)
g = √(10) units
g is the radius of the big circle.
h² = 2(6)²
h = 6√(2) units.
h is AC, the diagonal of the square, ABCD.
tanj = 2/6
j = atan(⅓)°
k = 45-j
k = (45-atan(⅓))°
cos(45-atan(⅓)) = l/√(10)
l = 2.8284271247 units.
l = 2√(2) units.
m = 2l
m = 5.6568542495 units.
m = 4√(2) units.
m is MC.
Therefore, the required length, AM is;
AM = AC-MC
AM = 6√(2)-4√(2)
AM = 2√(2) units.
AM = 2.8284271247 units.