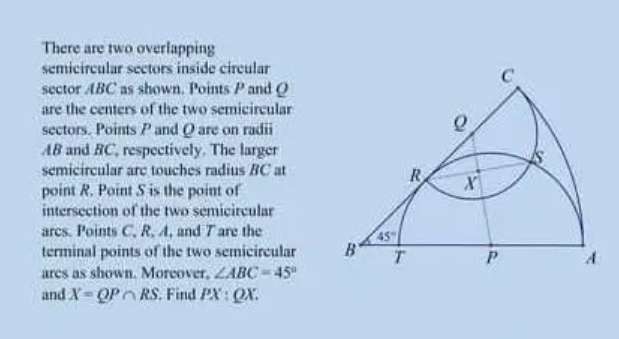
Mathematics Question and Solution
Let the radius of sector ABC be 2 units.
Therefore;
Calculating TP = PA = RP = BR, let it be x.
2x²=(2-x)²
x²+4x-4=0
x = (2√(2)-2) units.
Calculating RQ = QC, let it be y.
2y+x=2, and x = 2√(2)-2
2y=2-(2√(2)-2)
y = (2-√(2)) units.
Consider right-angled triangle PQR.
Angle RPQ is;
atan(1/√(2))°
Therefore;
Length PQ is;
(2-√(2))/(sin(atan(1/√(2)))
PQ = 1.01461187235 units.
Length PX is;
(2√(2)-2)cos(atan(1/√(2)))
PX = 0.6764079149 units.
Length QX will be;
PQ-PX
QX = 1.01461187235 - 0.6764079149
QX = 0.33820395745 units.
It implies;
PX : QX is;
0.6764079149 ÷ 0.33820395745
= 2