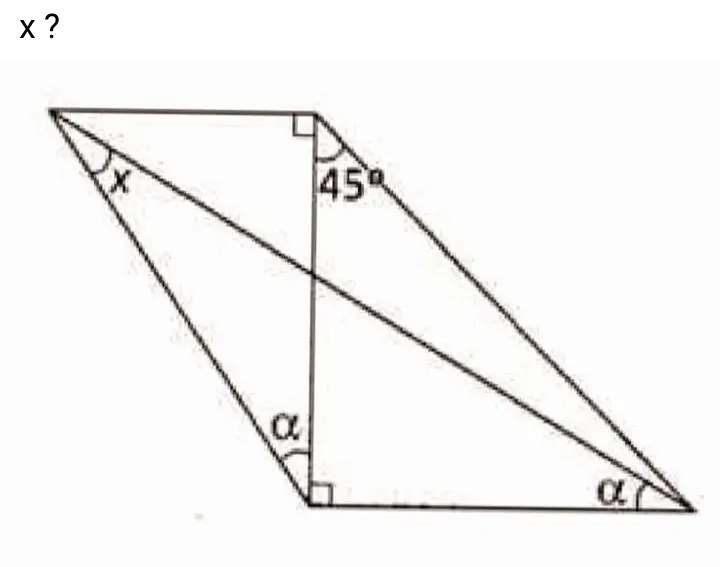
Mathematics Question and Solution
Calculating angle x.
Let the hypotenuse of the inscribed right-angled triangle of the ascribed quadrilateral be 1 unit.
2a² = 1²
a = √(1/2) units.
a = 0.7071067812 units.
c = (b+0.7071067812) units.
Observing similar right-angled triangle side length ratios.
0.7071067812 - (b+0.7071067812)
b - 0.7071067812
Cross Multiply.
b²+0.7071067812b = 0.5
b²+0.7071067812b-0.5 = 0
Resolving the above quadratic equation via completing the square approach to get b.
(b+0.3535533906)² = 0.5+0.3535533906²
(b+0.3535533906)² = 0.625
b = -0.3535533906±√(0.625)
b = -0.3535533906±0.790569415
b = 0.4370160244 units.
Recall.
c = (b+0.7071067812)
And b = 0.4370160244 units.
c = 0.4370160244+0.7071067812
c = 1.1441228056 units.
tand = 1.1441228056/0.7071067812
d = 58.2825255882°
tane = 0.4370160244/0.7071067812
e = 31.7174744081°
It implies;
x = d-e
x = 58.2825255882-31.7174744081
x = 26.5650511801°
x = atan(½)°