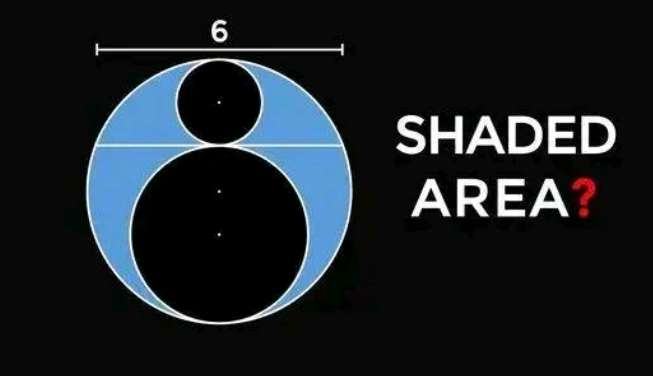
Mathematics Question and Solution
Let a be the radius of the ascribed circle.
a² = (0.5*6)²+b²
b = √(a²-9) units.
c = a-b
c = (a-√(a²-9)) units.
d = ½(c)
d = ½(a-√(a²-9)) units.
d is the radius of the small inscribed circle.
e = a+b
e = (a+√(a²-9)) units.
f = ½(e)
f = ½(a+√(a²-9)) units.
f is the radius of the big inscribed circle.
It implies;
f = 2d
½((a+√(a²-9))) = 2*½(a-√(a²-9))
((a+√(a²-9)) = 2(a-√(a²-9))
a+√(a²-9) = 2a-2√(a²-9)
a = 3√(a²-9)
a² = 3²(a²-9)
81 = 9a²-a²
8a² = 81
a = √(81/8)
a = 9/(2√(2))
a = ¼(9√(2)) units.
a = 3.1819805153 units.
Recall.
d = ½(a-√(a²-9)) units.
d is the radius of the small inscribed circle.
And a = 3.1819805153 units.
Therefore;
d = ½(3.1819805153-√(3.1819805153²-9))
d = 1.0606601718 units.
Again;
f = ½(a+√(a²-9)) units.
f is the radius of the big inscribed circle.
And a = 3.1819805153 units.
f = ½(3.1819805153+√(3.1819805153²-9))
f = 2.1213203435 units.
Therefore, shaded blue area is;
πa²-πd²-πf²
= π(3.1819805153)²-π(1.0606601718)²-π(2.1213203435)²
= 10.125π-1.125π-4.5π
= 10.125π-5.625π
= 4.5π square units.