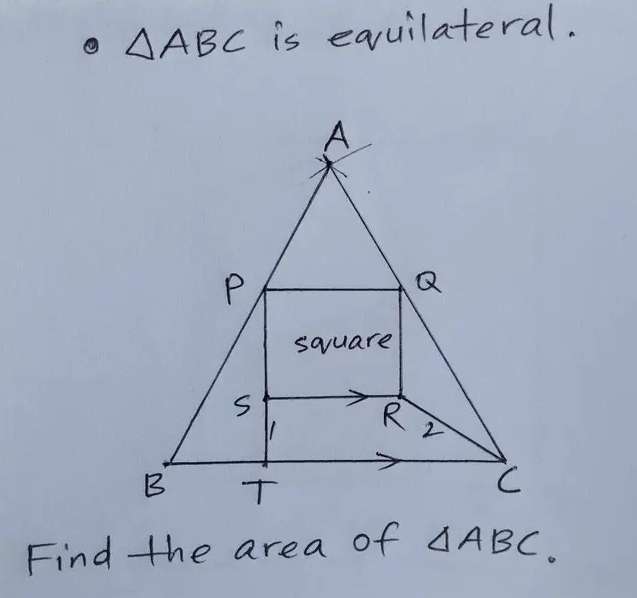
Mathematics Question and Solution
Let the inscribed square side length be a.
2² = 1²+b²
b² = 4-1
b = √(3) units.
c = 2b+a
c = (a+2√(3)) units.
c is BC.
d = (a+1) units.
sin60 = (a+1)/e
½√(3) = (a+1)/e
√(3)e = 2a+2
e = ⅓(2√(3)a+2√(3)) units.
e is CQ.
f = a+e
f = (a+⅓(2√(3)a+2√(3))) units.
f is AC.
Therefore, calculating a, side length of the square.
Equating c and f.
(a+2√(3)) = (a+⅓(2√(3)a+2√(3)))
2√(3) = ⅓(2√(3)a+2√(3))
6√(3) = 2√(3)a+2√(3)
2√(3)a = 6√(3)-2√(3)
2√(3)a = 4√(3)
a = 2 units.
Again,a is the side length of the inscribed square.
Therefore;
BC is;
c = BC = (a+2√(3)) units.
And a = 2 units.
Therefore:
BC = (2+2√(3)) units.
BC is the side length of the equilateral triangle.
It implies;
Area equilateral triangle ABC is;
½(2+2√(3))²sin60
= ½(4+8√(3)+12)*½√(3)
= ¼(16+8√(3))*√(3)
= √(3)(4+2√(3))
= (6+4√(3)) square units.
= 2(3+2√(3)) square units.