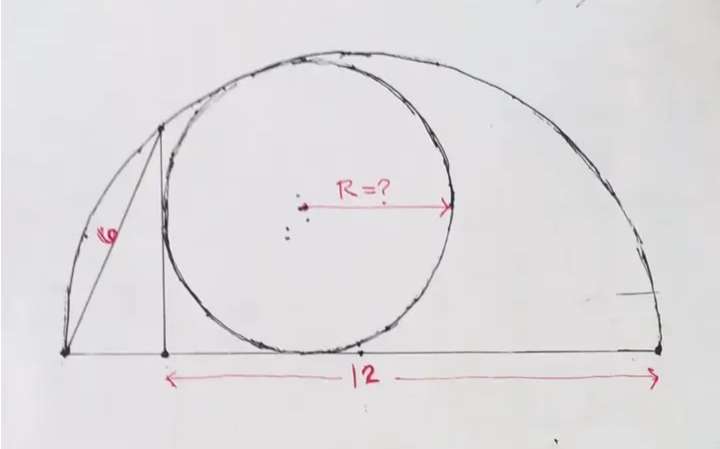
Mathematics Question and Solution
Calculating R, radius of the inscribed circle.
Observing similar plane shape (right-angled triangle) side length ratios.
(12+x) - 6
6 - x
Cross Multiply.
36 = 12x+x²
x²+12x-36 = 0
(x+6)² = 36+(+6)2
x = -6±√(72)
x = -6±6√(2)
x ≠ -6-6√(2)
x = 6√(2)-6
x = 6(√(2)-1) units.
x = 2.4852813742 units.
a = x+12
a = 6(√(2)-1)+12
a = 2.4852813742+12
a = 14.4852813742 units.
a is the diameter of the ascribed semi circle.
b = ½(a)
b = 0.5*14.4852813742
b = 7.2426406871 units.
b is the radius of the ascribed semi circle.
c = b-x-R
c = 7.2426406871-2.4852813742-R
c = (4.7573593129-R) units.
d = (7.2426406871-R) units.
Calculating R, radius of the inscribed circle.
d² = c²+R²
(7.2426406871-R)² = (4.7573593129-R)²+R²
52.4558441224-14.4852813742R+R² = 22.632467632-9.5147186258R+R²+R²
R²+4.9705627484R-29.8233764904 = 0
Resolving the above quadratic equation to get R.
R = 3.51472 units.