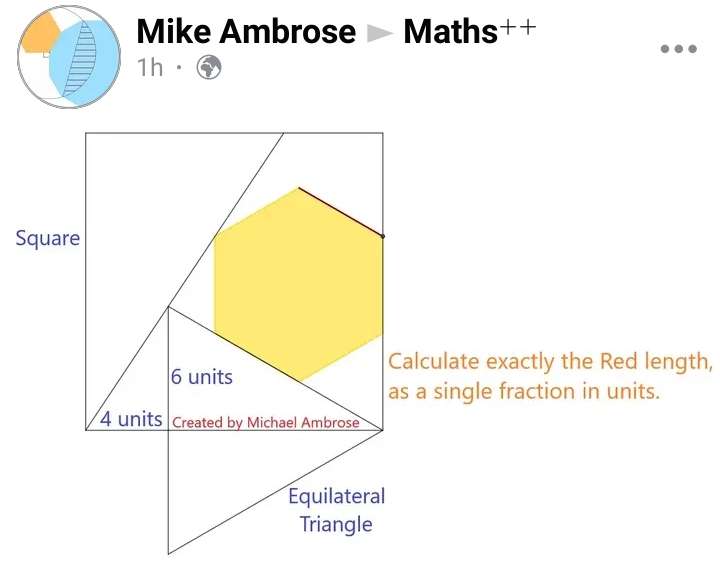
Mathematics Question and Solution
tan30 = 6/a
a = 6√(3) units.
b = (4+6√(3)) units.
b is the square side.
Let the side length of the inscribed regular hexagon be x (Red Length).
Calculating x.
c = (120-atan(⅔))°
d = 120-c
d = atan(⅔)°
It implies;
(x/sin(120-atan(⅔))) = (e/sin(atan(⅔)))
e = (4x/(2+3√(3))) units.
Therefore;
e+2x = 12
(4x/(2+3√(3)))+2x = 12
(4x+4x+6√(3)x)/(2+3√(3)) = 12
8x+6√(3)x = (24+36√(3))
x(4+3√(3)) = (12+18√(3))
x = (12+18√(3))/(4+3√(3))
x = (6(19-6√(3))/11) units.
x = (114-36√(3))/11 units.
x = 4.69510644796 units.