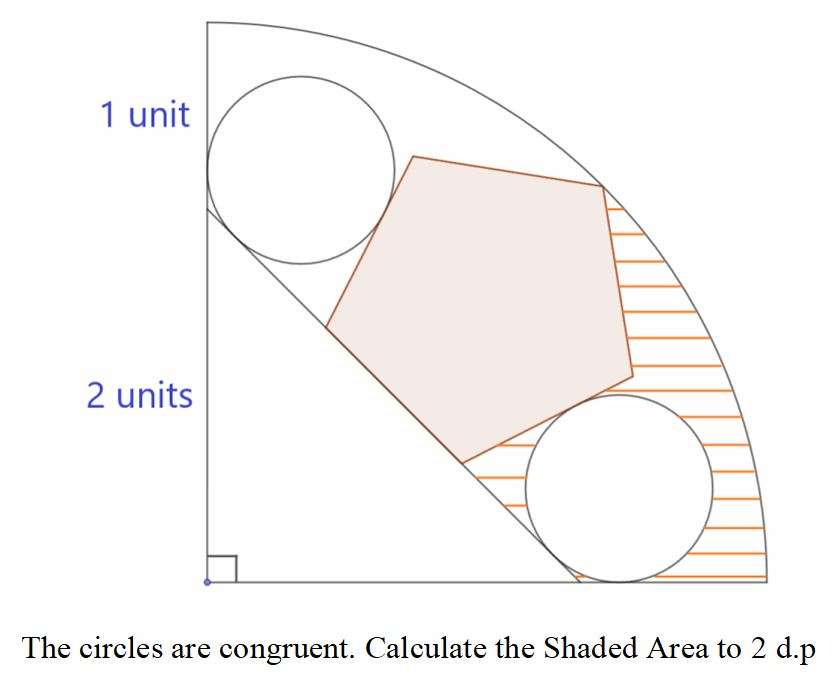
Mathematics Question and Solution
Sir Mike Ambrose is the author of the question.
a² = 2²+2²
a = 2√(2) units.
2b² = 4
b = √(2) units.
c = 3-√(2) units.
Let the side of the inscribed regular pentagon be d.
Calculating d.
e = ⅕(180*3)
e = 108°
f = ½(180-108)
f = 36°
(g/sin108) = (d/sin36)
g = 1.61803398875d units.
(1.61803398875d)² = (3-√(2))²+(d/2)²
d = 1.03050649521 units.
Where d is the side length of the regular pentagon.
g = 1.61803398875d
g = 1.61803398875*1.03050649521
g = 1.66739453488 units.
h = ½(2√(2)-1.03050649521)
h = 0.89896031477 unit.
i = ½(180-108)
i = 36°
j = ½(180-45)
j = 67.5°
k = 180-i-j
k = 76.5°
(l/sin36) = (0.89896031477/sin76.5)
l = 0.54341007916 unit.
Let r be the radius of the two congruent inscribed circles.
Calculating r.
sin67.5 = r/0.54341007916
r = 0.5020454499 unit.
It implies;
Area Shaded to 2 decimal places is;
Area sector with radius 3 units and angle 45° - Area triangle with height (3-√(2)) units and base 0.5152532476 units - Area triangle with height 1.03050649521 units and base 1.03050649521sin108 units - Area triangle with height and base √(2) units respectively - Area circle with radius 0.5020454499 units.
= 3.53429173529 - 0.40854080599 - 0.5049842078 - 1 - 0.5020454499
= 0.82892944372 square units.
≈ 0.83 square units.