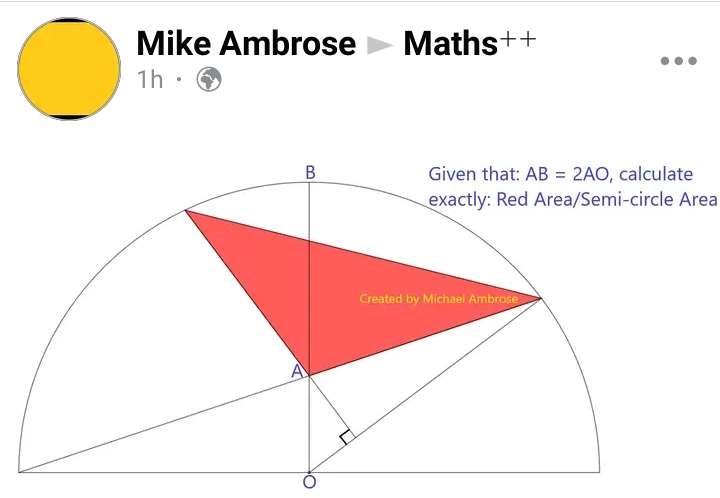
Mathematics Question and Solution
Let AO be 1 unit.
AB will be 2 units.
Therefore, radius r of the ascribed semi circle is;
= 3 units.
Area semi circle is;
½(3²)π
= ½(9π) square units.
tana = (1/3)
a = atan(⅓)°
b = (180-2atan(½))°
c = b-90
c = (180-2atan(⅓)°))-90
c = (90-2atan(⅓))°
sin(90-2atan(⅓)) = d/1
d = (4/5) units.
cos(90-2atan(⅓)) = e/1
e = (3/5) units.
f = r-e
f = 3-(3/5)
f = (12/5) units.
g² = 3²-(3/5)²
g² = 9-(9/25)
g = ⅕(6√(6)) units.
h = g-d
h = ⅕(6√(6))-(4/5)
h = ⅕(6√(6)-4) units.
j² = d²+f²
j² = (4/5)²+(12/5)²
j = √(160/25)
j = ⅘(√(10)) units.
k = atan(3)+(90-(90-2atan(⅓)))
k = atan(3)+2atan(⅓)
k = (90+atan(⅓))°
Therefore;
Area Red is;
0.5*⅘(√(10))*⅕(6√(6)-4)sin(90+atan(⅓))
= 6(6√(6)-4)/25 square units.
Therefore;
Area Red ÷ Area Semi Circle exactly is;
(6(6√(6)-4)/25)÷(9π/2)
= (4(6√(6)-4)/75π)
= 8(3√(6)-2)/75π