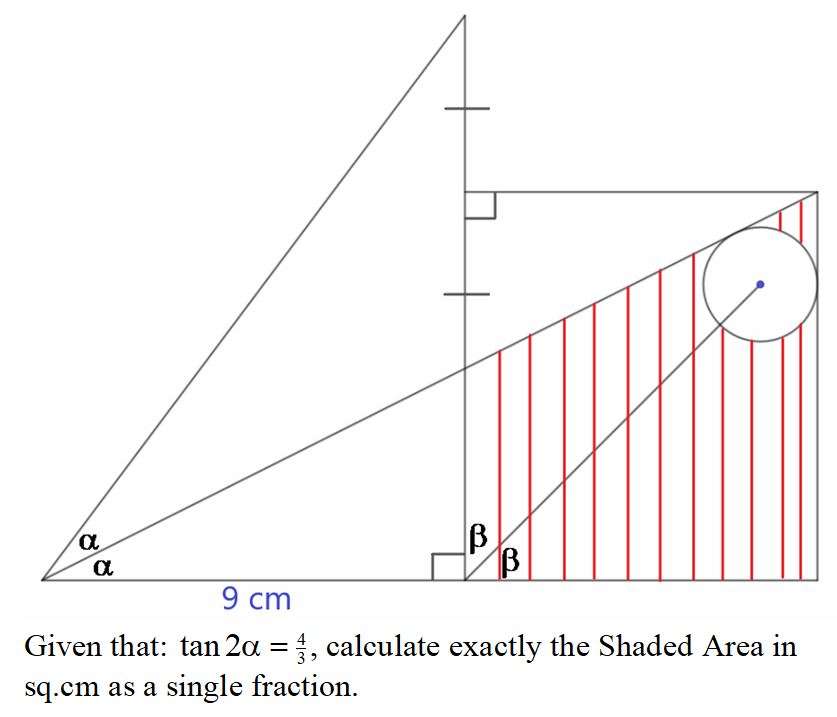
Mathematics Question and Solution
Sir Mike Ambrose is the author of the question.
⅓(4) = a/9
a = 12 cm.
let alpha be b.
Calculating b.
(2tanb/(1-tan²b)) = (4/3)
2tan²b+3tanb-2= 0
b = atan(½)°
½ = c/9
c = 4.5 cm.
d = ½(12-c)
d = 3.75 cm.
½ = 3.75/e
e = 7.5 cm
f² = 8.25²+7.5²
f = 11.14955156049 cm.
g = ½(90-atan(½))°
g = 31.71747441146°
h = 90-31.71747441146-atan(8.25/7.5)
h = 10.55621459463°
Let r be the radius of the inscribed circle.
sin31.71747441146 = r/i
i = 1.90211303259r
j² = 2(7.5-r)²
j = 7.5√(2)-√(2)r
It implies;
(7.5√(2)-√(2)r)² = (1.90211303259r)²+11.14955156049²-2*11.14955156049*1.90211303259rcos10.55621459463
112.5-30r+2r² = 3.61803398875r²+124.31250000002-41.69756081437r
1.61803398875r²-11.69756081437r+11.8125 = 0
r = 1.21353 cm
It implies;
Area Shaded in cm² exactly in decimal is;
Area trapezoid with parallel sides 4.5 cm and 8.25 cm, and height 7.5 cm - Area circle with radius 1.21353 cm.
½*7.5(8.25+4.5) - π(1.21353)²
= (765/16) - 4.6264823206
= 43.1860176794 cm²
Exactly as a single fraction is;
539825221/12500000 cm²