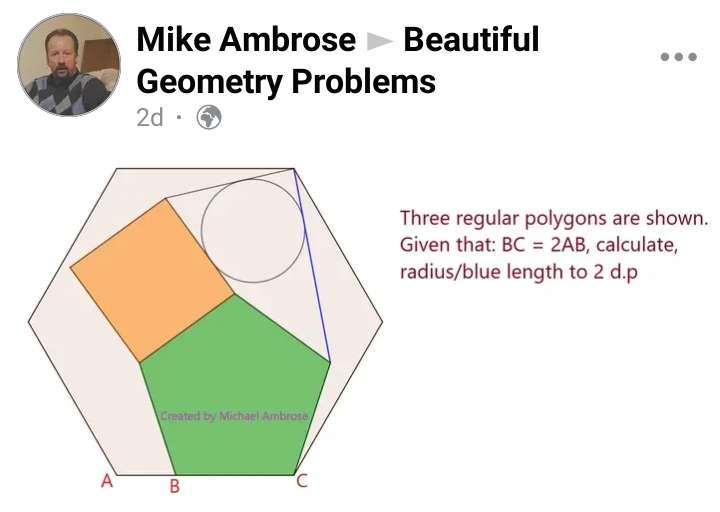
Mathematics Question and Solution
Let AB be 1 unit.
Therefore;
BC = 2 units.
It implies, the regular hexagon side length is 3 units.
a = 120-108
a = 12°
b² = 2²+3²-2*2*3cos12
b = 1.1234895599 units.
(1.1234895599/sin12) = (2/sinc)
c = 21.72287686377°
d = 120-c
d = 120-21.72287686377
d = 98.27712313623°
Calculating Length Blue.
Let it be e.
e² = 3²+1.1234895599²-2*3*1.1234895599cos98.27712313623
e = 3.35151630086 units.
f = 180-12-21.72287686377
f = 146.27712313623°
(3.35151630086/sin98.27712313623) = (3/sing)
g = 62.34928014497°
h = 360-108-62.34928014497-146.27712313623
h = 43.3735967188°
j² = 2²+2²-8cos162
j = 3.95075336238 units.
k = ½(180-162)
k = 9°
l = 43.3735967188-9
l = 34.3735967188°
m² = 3.95075336238²+3.35151630086²-2*3.95075336238*3.35151630086cos34.3735967188
m = 2.23238484728 units.
(2.23238484728/sin34.3735967188) = (3.95075336238/sinn)
n = 87.6722960695°
o = 180-34.37359671894-87.6722960695
o = 57.95410721156°
p = ½(n)
p = 0.5*87.6722960695
p = 43.83614803475°
q = ½(o+9)
q = 0.5(57.95410721156+9)
q = 33.47705360578°
Calculating r, radius of the inscribed circle.
(r/tan33.47705360578)+(r/tan43.83614803475) = 2.23238484728
2.55362491876r = 2.23238484728
r = 2.23238484728÷2.55362491876
r = 0.8742023274 units
Therefore;
Radius ÷ Length Blue to 2 decimal places is;
0.8742023274÷3.35151630086
= 0.26083785634
≈ 0.26