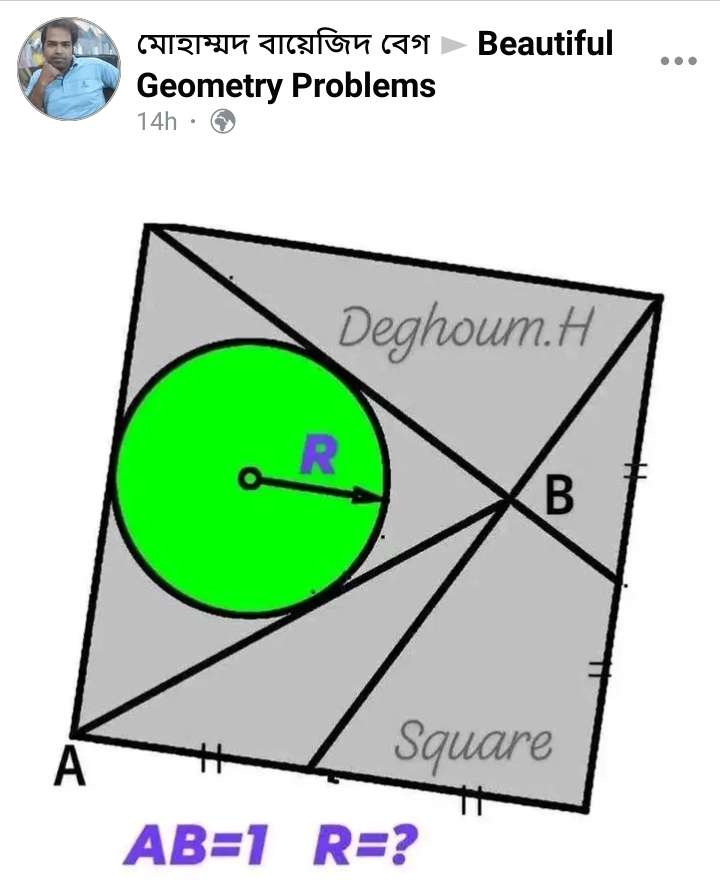
Mathematics Question and Solution
Let the square side be 2a units.
b² = (2a)²+a²
b = √(5a²)
b = √(5)a units.
cos(atan(½)) = c/a
c = ⅕(2√(5))a unit.
d = b-c
d = √(5)a-⅕(2√(5))a
d = ⅕(3√(5))a units.
Calculating a.
1 = a²+ (⅕(3√(5))a)²-2a(⅕(3√(5))a)cos(180-atan(2))
1 = (14a²/5)+(6a²/5)
14a²+6a² = 5
20a² = 5
a = ½ units.
2a (the square side length) = 1 unit.
(1/sin(180-atan2)) = (0.5/sine)
e = 26.56505117708°
f = 180-(180-atan(2))-26.56505117708
f = 36.86989764584°
g = 90-36.86989764584
g = 53.13010235416°
h = atan(2)°
Calculating r, inscribed green circle's radius.
(r/tan(0.5atan(2)))+(r/tan(0.5*53.13010235416)) = 1
1.61803398875r+2r = 1
3.61803398875r = 1
r = 0.27639320225 units
Where;
r = R = radius of the inscribed green circle.