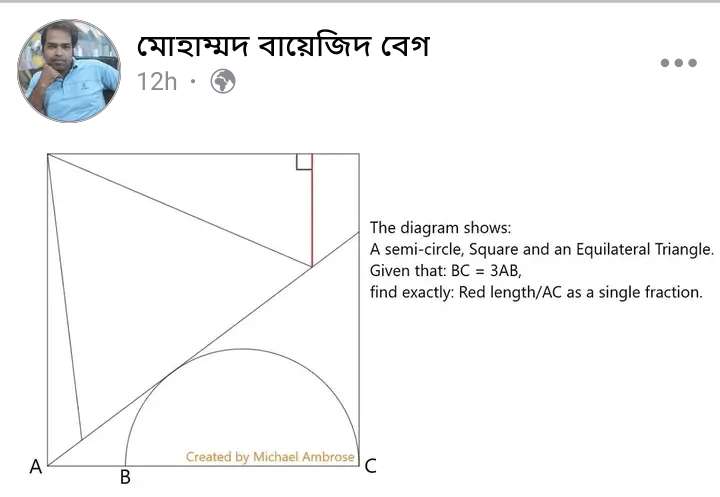
Mathematics Question and Solution
Let AB be 1 unit.
BC = 3 units.
It implies;
AC = 1+3
AC = 4 units.
AC is a side length of the square.
Radius of the inscribed half circle a is;
½(BC)
a = ½(3) units.
a = 1.5 units.
b = 1.5+AB
b = 1.5+1
b = 2.5 units.
b = ½(5) units.
c²+(1.5)² = (2.5)²
c² = 2.5²-1.5²
c = 2 units.
Considering similar triangle ratios.
2 = 4
1.5 = d
Cross Multiply.
d = 3 units.
tane = (3/4)
e = atan(3/4)°
f = atan(4/3)°
Calculating g, side length of the regular triangle.
(4/sin120) = (g/sin(atan(4/3)))
g = (32√(3)/15) units.
h = 180-120-atan(4/3)
h = (60-atan(4/3))°
j = 90-60-(60-atan(4/3))
j = (atan(4/3)-30)°
Red length is;
Let it be k.
sin(atan(4/3)-30) = k/(32√(3)/15)
k = (32√(3)/15)sin(atan(4/3)-30)
k = 16(4-√(3))/25 units.
Red Length ÷ AC.
= 16(4-√(3))/25 ÷ 4
= 4(4-√(3))/25 ÷ 1
= (16-4√(3))/25