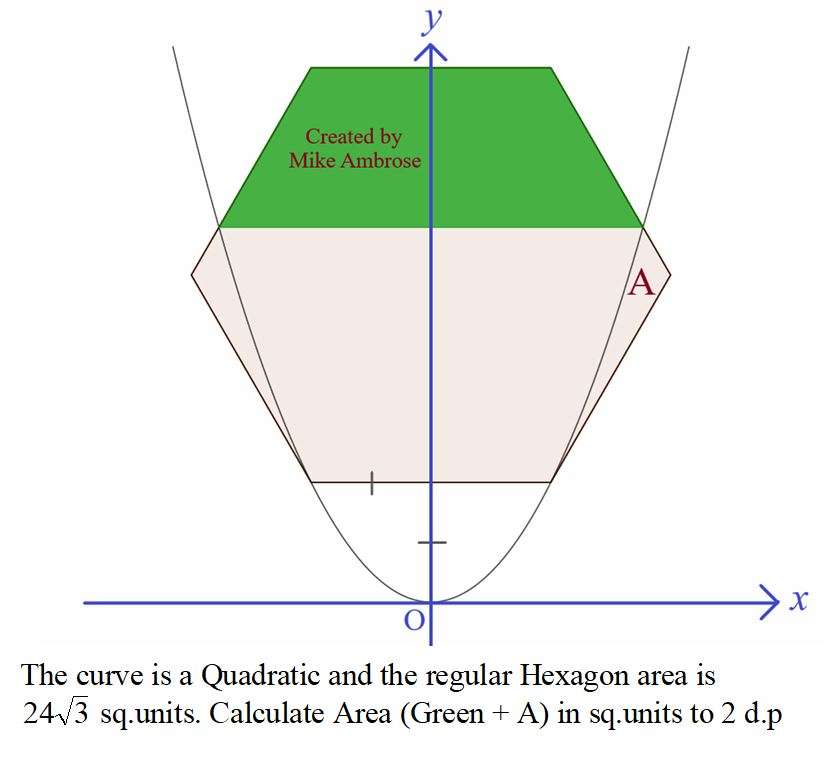
Mathematics Question and Solution
Notice;
Hexagon Area = 24√(3) square units.
Calculating hexagon side length.
Let it be a.
(6a²)/(4tan30) = 24√(3)
½(3√(3))a² = 24√(3)
3a² = 48
a = 4 units.
Equation of the curve is;
y = ½(x²) ------ (1).
sin60 = b/4
b = 2√(3) units.
cos60 = c/4
c = 2 units.
Gradient = ((4√(3)+2)-(2√(3)+2))/(2-4)
Gradient = -√(3)
(y-(4√(3)+2))/(x-2) = -√(3)
y = -√(3)x+6√(3)+2 ---- (2).
Equation (1) and (2).
½(x)² = -√(3)x+6√(3)+2
x = 3.53906
y = ½(3.53906)²
y = 6.2624728418
d = 2(3.53906)
d = 7.07812 units.
e = 4 - 3.53905
e = 0.46095 unit.
f = (4√(3)+2)-6.2624728418-
f = 2.66573038848 units.
Area Green is;
½*2.66573038848(4+7.07812)
= 14.76564056561 square units.
Calculating Area A.
(Area under the curve at x = 2 and x = 3.53906) + ½*0.46095(2√(3)+2+6.2624728418) - ½*2(4+2√(3))
= 6.0544223785 + 2.70268224796 - 7.46410161514
= 1.29300301132 square units.
It implies;
Area Green + Area A to 2 decimal places square units is;
14.76564056561+1.29300301132
= 16.05864357693 square units.
≈ 16.06 square units.