Mathematics Question and Solution
Let the radius of the large circle be 1 unit.
Diameter of the large circle = 2 units.
sin60 = 2/a
a = ⅓(4√(3)) units.
Where a is the side length of triangle ABC.
b² = 2-2cos
b = √(3) units.
c = a-b
c = ⅓(√(3)) units.
(d/sin50) = (4√(3)/(3sin100))
d = 1.79639514045 units.
e² = (⅓(2√(3)))²+1²
e = ⅓√(21) units.
1² = (⅓√(21))²+f²-2*⅓√(21)f cos(atan(3/(2√(3))-10)
f² - 2.62161244054f + 1.33333333333 = 0
f = 1.93113 units.
g² = 1.93119²+(⅓(4√(3)))²-2*1.93119(⅓(4√(3)))cos10
g = 0.52778327773 unit.
(0.52778327773/sin10) = (1.93113/sinh)
h = 39.44883273038°
i = 60-h
i = 20.55116726962°
j = 120-i
j = 99.44883273038°
(k/sin60) = (4√(3)/(3sin99.44883273038))
k = 2.0275080083 units.
l² = 2.0275080083²+(4√(3)/3)²-2*2.0275080083(4√(3)/3)cos20.55116726962
l = 0.82185113743 unit.
Let the radius of the small circle be r.
Calculating r.
m = √(3)-0.82185113743
m = 0.91019967014 unit.
n² = 0.91019967014²+1-2*0.91019967014cos30
n = 0.50194757277 unit.
(0.50194757277/sin30) = (1/sino)
o = 84.9511110217°
p = 30+(180-o)
p = 125.0488889783°
1² = q²+0.50194757277²-2*0.50194757277qcos125.0488889783
q²+0.57651207375- 0.74804863419 = o
q = 0.623413 unit.
s² = 0.623413²+0.82185113743²-2*0.82185113743*0.623413cos30
s = 0.42031200563 unit.
(0.42031200563/sin30) = (0.623413/sint)
t = 47.86852326995°
r is;
(r/tan15) + (r/(0.5tan47.86852326995)) = 0.82185113743
r = 0.14831682181 unit.
Therefore;
Radius small ÷ Radius large to 2 decimal places is;
0.14831682181 ÷ 1
= 0.14831682181
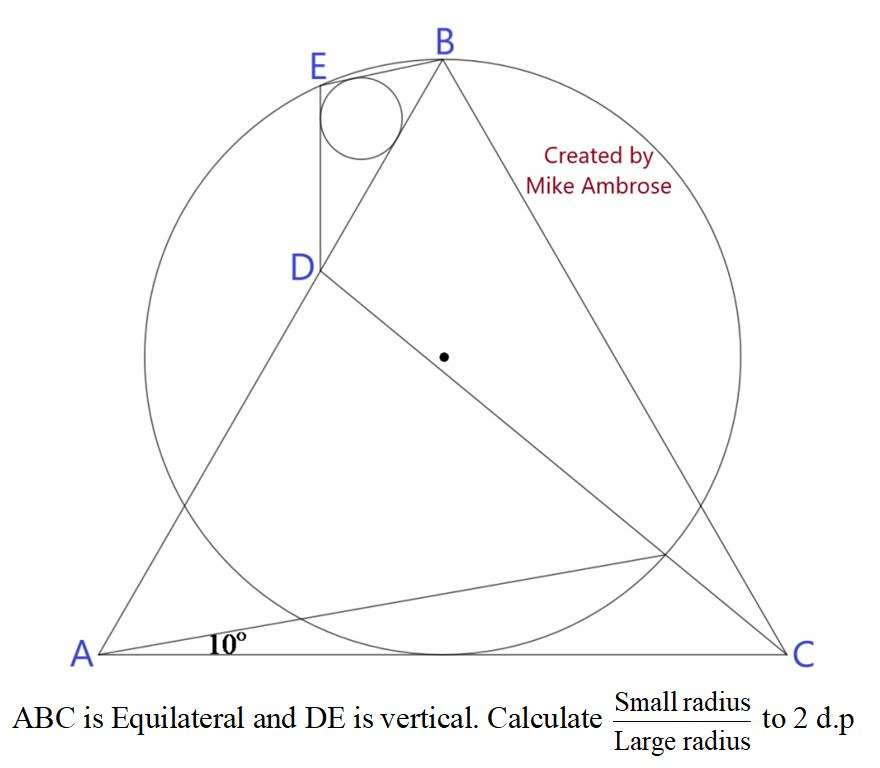
≈ 0.15