Mathematics Question and Solution
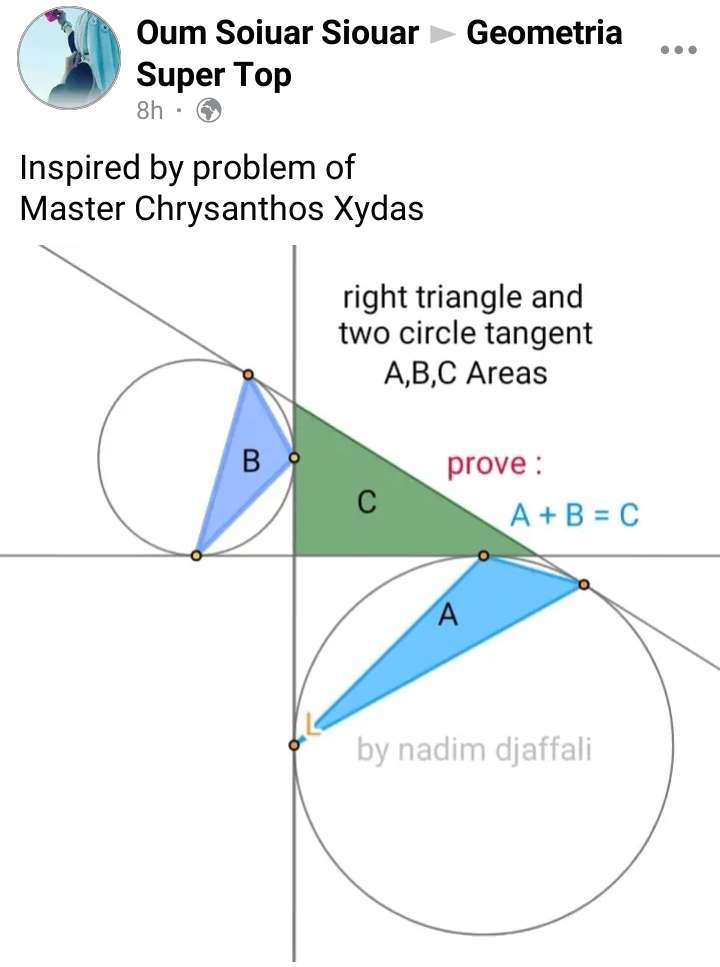
Let the height and base of area triangle C be 2 units and 3 units respectively.
Therefore;
Area Triangle C is;
½*2*3
= 3 square units.
tana = (2/3)
a = atan(2/3)°
b = 189-a
b = 180-atan(2/3)
b = 146.30993247402°
c = ½(180-146.30993247402)
c = 16.84503376299°
Let the radius of the big circle be d.
Calculating d.
e = ½(146.30993247402)
e = 73.15496623701°
f = (3-d) units.
tan73.15496623701 = d/(3-d)
d = 9.9083269132-3.30277563773d
4.30277563773d = 9.9083269132
d = 9.9083269132/4.30277563773
d = 2.30277563773 units.
g = 3-d
g = 3-2.30277563773
g = 0.69722436227 units.
(0.69722436227/sin16.84503376299) = (h/sin146.30993247402)
h = 1.33461575561 units.
j² = 2d²
j² = 2(2.30277563773)²
j = 3.25661653798 units.
k = 180-45-16.84503376299
k = 118.15496623701°
Therefore, area triangle A is;
0.5*3.25661653798*1.33461575561sin118.15496623701
= 1.91602514718 square units.
Calculating area triangle B
l = 180-atan(3/2)
l = 123.69006752598°
m = ½(180-123.69006752598)
m = 28.15496623701°
n = ½(123.69006752598)
n = 61.84503376299°
Let the radius of the small circle be o.
Therefore;
tan61.84503376299 = o/(2-o)
o = 3.73703418364-1.86851709182o
2.86851709182o = 3.73703418364
o = 3.73703418364/2.86851709182
o = 1.30277563773 units.
p = 2-o
p = 2-1.30277563773
p = 0.69722436227 units.
q² = 2*0.69722436227²-2*0.69722436227²cos123.69006752598
q = 1.22945001971 units.
r² = 2o²
r² = 2(1.30277563773)²
r = 1.84240297561 units.
s = 190-45-28.15496623701
s = 106.84503376299°
Area Triangle B is;
0.5*1.84240297561*1.22945001971sin106.84503376299
= 1.08397485283 square units.
Notice;
Triangle A + Triangle B Must Equal Triangle C.
Triangle C = 3 square units.
Therefore;
Triangle A + Triangle B is;
1.91602514718+1.08397485283
= 3 square units.
Proved.