Mathematics Question and Solution
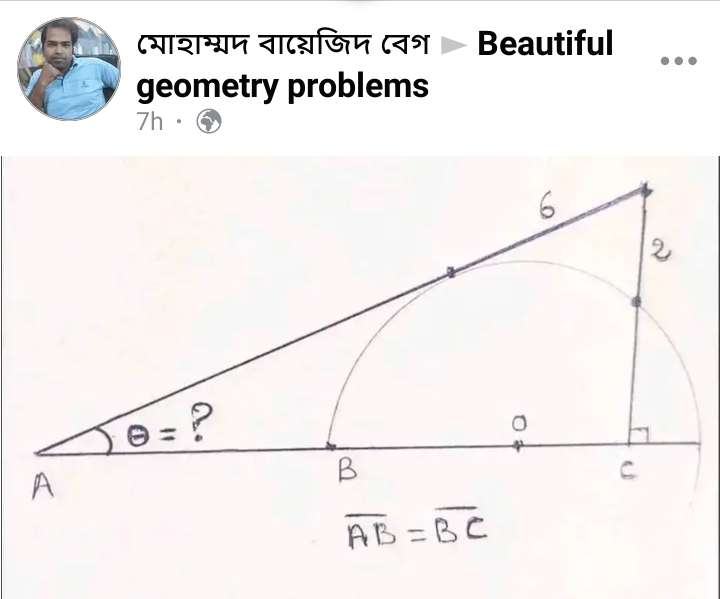
Let AB = x
Let r be the radius of the semi circle.
It implies;
OC = x-r
y = √(r²-(x-r)²)
y = √(r²-(x²-2xr+r²))
y = √(2xr-x²)
Therefore;
6²+r² = (x-r)²+(2+√(2xr-x²))²
6²+r² = x²-2xr+r²+4+4√(2xr-x²)+2xr-x²
6²+r² = r²+4+4√(2xr-x²)
32 = 4√(2xr-x²)
8 = √(2xr-x²)
64 = 2xr-x²
64+x² = 2xr
r = (64+x²)/(2x) -------- (1)
z = √((x+r)²-r²)
z = √(x²+2xr+r²-r²)
z = √(x²+2xr)
It implies;
(√(x²+2xr)+6)² = (2x)²+(2+√(2xr-x²))²
x²+2xr+12√(x²+2xr)+36 = 4x²+4+4√(2xr-x²)+2xr-x²
2x²+12√(x²+2xr)+32 = 4x²+4√(2xr-x²)
12√(x²+2xr)+32 = 2x²+4√(2xr-x²)
Dividing through by 2.
6√(x²+2xr)+16 = x²+2√(2xr-x²) ------ (2)
Calculating x.
Substituting (1) in (2).
6√(x²+2x((64+x²)/(2x))+16 = x²+2√(2x((64+x²)/(2x))-x²)
6√(x²+64+x²)+16 = x²+2√(64+x²-x²)
6√(2x²+64)+16 = x²+16
6√(2x²+64) = x²
36(2x²+64) = x⁴
x⁴-72x²-2304 = 0
Let x² = t
Therefore;
t²-72t-2304 = 0
It implies;
t ≠ -24
t = 96
And x² = t
Therefore;
x² = 96
x = √(96)
x = √(16*6)
x = 4√(6) units.
And x = AB = BC.
Therefore;
AB = BC = 4√(6) units.
At (1).
r = (64+x²)/(2x)
Substituting the value of x = AB = BC in (1) to get r.
r = (64+(4√(6))²)/(2(4√(6)))
r = (64+96)/(8√(6))
r = 160/(8√(6))
r = 20/√(6)
r = ⅓(10√(6)) units.
The required angle theta is;
Let it be a.
sina = (r/(x+r))
sina = ⅓(10√(6))/(⅓(10√(6))+4√(6))
sina = (⅓(10√(6)))/(⅓(22√(6)))
sina = (10/22)
sina = 5/11
a = asin(5/11)°
a = 27.03569178941°
Or
The base of the right-angled triangle is;
AC = 2(AB)
AC = 8√(6) units.
The height of the right-angled triangle is;
2+y
y = √(2xr-r²)
And x = 4√(6), r = ⅓(10√(6)).
height = 2+√(2*4√(6)*⅓(10√(6))-(4√(6))²)
= 2+√(160-96)
= 2+√(64)
= 10 units.
Therefore the required angle theta is;
Let it be a.
tana = 10/(8√(6))
tana = 5√(6)/24
a = atan(5√(6)/24)
a = 27.03569178941°